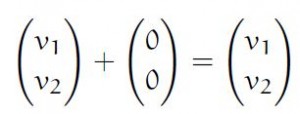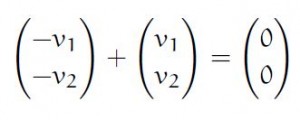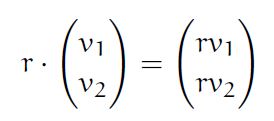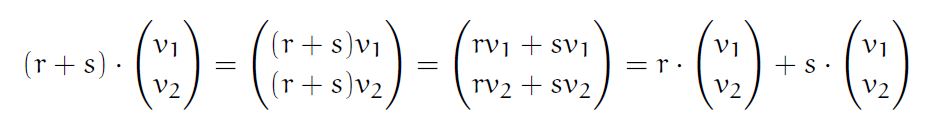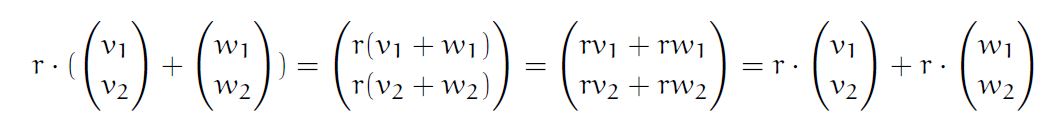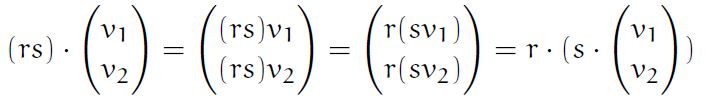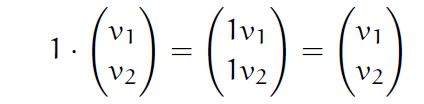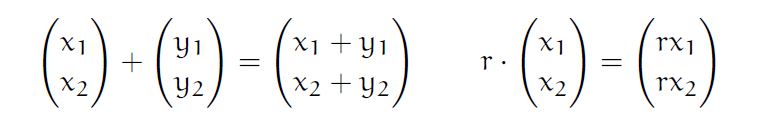Vector space is a set of “vectors” with a notion of Addition such that:
- V is closed under addition
- V is commutative
- V is associative
- For every A there is a zero vector such that [V+0=V]
- For all Vectors in V there is a -V such that (-V)+V=0
And of a Scalar Multiplication such that:
- V is closed under Scalar Multiplication
- For All r,s are a set of real numbers and V is a Vector then (r+s)V= rV+sV
- r is a set of real numbers and V, W are vectors, r(V+W)= rV+rW
- r,s are a set of real numbers and V is a vector, (rs)V=r(sV)
- 1*V=V
Proofs:
- Two vector after adding are still a vector, the commute a because they have same number of column array.
- The order of adding the vectors doesn’t affect the result
- (V+W)+U=V+(W+U) the parenthesis doesn’t affect the result